Aturan cosinus menjelaskan hubungan antara kuadrat panjang sisi dengan nilai cosinus dari salah satu sudut pada segitiga.
Lebih jelasnya pada gambar dibawah ini.
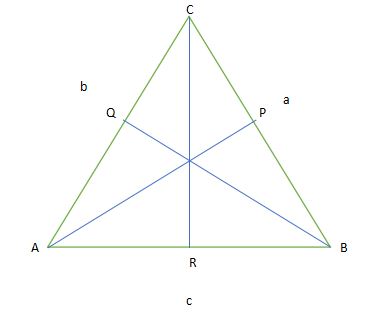
Keterangan
Perhatikan segitiga BCR
Sin B = CR/a maka CR = a sin B
Cos B = BR/a maka BR = a cos B
AR = AB – BR = c – a cos B
Perhatikan segitiga ACR
b2 = AR2 + CR2
b2 = (c – a cos B)2 + (a sin B)2
b2 = c2 – 2ac cos B + a2 cos2 B + a2 sin2 B
b2 = c2 – 2ac cos B + a2 (cos2 B + sin2 B)
b2 = c2 + a2– 2ac cos B
Menggunakan analogi yang sama, kemudian diperoleh aturan cosinus untuk segitiga ABC sebagai berikut
a2 = c2 + b2– 2bc cos A
b2 = a2 + c2 – 2ac cos B
c2 = a2 + b2 – 2ab cos C
Contoh Soal Aturan Cosinus
Diketahui sebuah segitiga ABC memiliki sisi dengan panjang
a = 10 cm
c = 12 cm
besar sudut B = 60̊.
Hitung panjang sisi b!
b2 = a2 + c2 – 2ac cos B
b2 = 100 + 144 – 44 cos 60̊
b2 = 244 – 44(0,5)
b2 = 244 – 22
b2 = 222
b = 14,8997
Jadi, panjang sisi b adalah 14,8997 cm
Lebih jelasnya pada gambar dibawah ini.

Keterangan
- A = besar sudut di hadapan sisi a
- a = panjang sisi a
- B = besar sudut di hadapan sisi b
- b = panjang sisi b
- C = besar sudut di hadapan sisi c
- c = panjang sisi c
- AP ┴ BC
- BQ ┴ AC
- CR ┴ AB
Perhatikan segitiga BCR
Sin B = CR/a maka CR = a sin B
Cos B = BR/a maka BR = a cos B
AR = AB – BR = c – a cos B
Perhatikan segitiga ACR
b2 = AR2 + CR2
b2 = (c – a cos B)2 + (a sin B)2
b2 = c2 – 2ac cos B + a2 cos2 B + a2 sin2 B
b2 = c2 – 2ac cos B + a2 (cos2 B + sin2 B)
b2 = c2 + a2– 2ac cos B
Menggunakan analogi yang sama, kemudian diperoleh aturan cosinus untuk segitiga ABC sebagai berikut
a2 = c2 + b2– 2bc cos A
b2 = a2 + c2 – 2ac cos B
c2 = a2 + b2 – 2ab cos C
Contoh Soal Aturan Cosinus
Diketahui sebuah segitiga ABC memiliki sisi dengan panjang
a = 10 cm
c = 12 cm
besar sudut B = 60̊.
Baca Juga
Hitung panjang sisi b!
b2 = a2 + c2 – 2ac cos B
b2 = 100 + 144 – 44 cos 60̊
b2 = 244 – 44(0,5)
b2 = 244 – 22
b2 = 222
b = 14,8997
Jadi, panjang sisi b adalah 14,8997 cm
HALAMAN SELANJUTNYA:


ConversionConversion EmoticonEmoticon