Aturan sinus berbunyi bahwa perbandingan panjang sisi sebuah segitiga dengan sinus sudut yang menghadapnya memiliki nilai yang sama.
Lebih jelasnya pada gambar dibawah ini
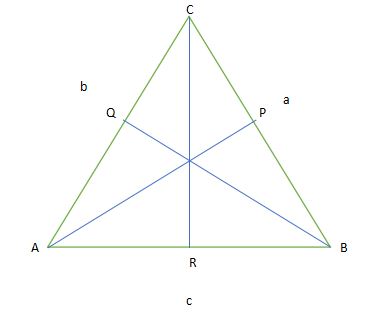Keterangan
A = besar sudut di hadapan sisi a
a = panjang sisi a
B = besar sudut di hadapan sisi b
b = panjang sisi b
C = besar sudut di hadapan sisi c
c = panjang sisi c
AP ┴ BC
BQ ┴ AC
CR ┴ AB
Perhatikan segitiga ACR
Sin A = CR/b maka CR = b sin A …(1)
Perhatikan segitiga BCR
Sin B = CR/a maka CR = a sin B …. (2)
Perhatikan segitiga ABP
Sin B = AP/c maka AP = c sin B … (3)
Perhatikan segitiga APC
Sin C = AP/b maka AP = b sin C …(4)
Berdasarkan persamaan (1) dan (2) didapat
CR = b sin A = a sin B maka a/sin A = b/sin B …(5)
Berdasarkan persamaan (3) dan (4) didapat
AP = c sin B = b sin C maka b/sin B = c/sin C …(6)
Kemudian, berdasarkan persamaan (5) dan (6) diperoleh
a/sin A = b/sin B = c/sin C
Persamaan ini yang kemudian disebut dengan aturan sinus.
Contoh Soal Aturan Sinus
1. Andi sedang mengukur mainan segitiganya yang tiap sudutnya dikodekan dengan A, B, dan C, kemudian diketahui segitiga tersebut memiliki sudut A = 30º, sisi a = 6cm dan sisi b = 8cm. Hitung besar sudut B!
Pembahasan
Akan dicari besar sudut B
sin B = (b sin A)/a
sin B = 8/6 sin 30̊
sin B = 2/3
B = arc sin B
B = arc sin (2/3)
B = 41,8̊
Jadi, besar sudut B adalah 41,8̊ atau 180̊ – 41,8̊ = 138,2̊
2. Sebuah segitiga ABC memiliki panjang AC = 4 cm. Jika besar ∠ ABC = 60º dan ∠BAC = 30º, maka panjang BC = … cm.
Pembahasan
AC/sin ∠ABC = BC/sin∠BAC
4cm/sin 60 = BC/sin30
4cm/½√3 = BC/½
BC = ½ × 4cm/½√3
BC = 4cm/√3
BC = 4/3 √3 cm
Jadi, panjang BC adalah BC4/3 √3cm.
3. Diketahui sebuah segitiga ABC dengan panjang AB = 9cm dan BC = 12cm. Jika besar ∠ ABC = 30º, tentukan luas segitiga ABC!
Pembahasan
L = ½ a t
Sin ∠ABC = t/BC
t = BC × Sin ∠ABC
Sehingga diperoleh
L = ½ a t
L = ½ × AB × BC × Sin ∠ABC
L = ½ × 9cm × 12cm × Sin 30o
L = ½ × 9cm × 12cm × ½
L = 27cm2
Sin ∠ABC = t/AB
t = AB × Sin ∠ABC
Sehingga diperoleh
L = ½ a t
L = ½ × BC × AB × Sin ∠ABC
L = ½ × 12cm × 9cm × Sin 30o
L = ½ × 12cm × 9cm × ½
L = 27cm2
Jadi, luas segitiga ABC adalah 27cm2.
4. Diketahui sebuah segitiga PQR memiliki luas sebesar 96cm2. Jika panjang PR = 12cm dan besar ∠PRQ = 60º, tentukan panjang QR!
Pembahasan
L = ½ × PR × QR × Sin ∠PRQ
96cm2 = ½ × 12cm × QR × Sin 60o
96cm2 = ½ × 12cm × QR × ½√3
96cm2 = 4√3cm × QR
QR = 96cm2 ÷ 4√3cm
QR = 24/√3 cm
QR = 8√3cm
Jadi, panjang QR adalah 8√3cm.
5. Sebuah segitiga XYZ memiliki panjang XZ = 6cm dan YZ = 2√3cm. Jika besar ∠ XYZ = 60º, tentukan besar ∠YXZ !
Pembahasan
XZ/sin ∠XYZ = YZ/sin∠YXZ
6cm/sin 60 = 2√3cm/sin∠YXZ
6cm/½√3 = 2√3cm/sin∠YXZ
sin∠YXZ = 2√3cm × ½√3 ÷ 6cm
sin∠YXZ = 3/6
sin∠YXZ = ½
YXZ = arc sin (½)
YXZ = 30º
Jadi, besar ∠YXZ adalah 30º.
6. Diketahui sebuah segitiga ABC memiliki luas sebesar 6cm2. Jika panjang AB = 3cm dan BC = 4cm, tentukan besar ∠ABC!
pembahasan
L = ½ × AB × BC × Sin ∠ABC
6cm2 = ½ × 3cm × 4cm × Sin ∠ABC
6cm2 = 6cm2 × Sin ∠ABC
Sin ∠ABC = 1
ABC = arc sin (1)
ABC = 90º
Jadi, besar ∠ABC adalah 90º.
Lebih jelasnya pada gambar dibawah ini
A = besar sudut di hadapan sisi a
a = panjang sisi a
B = besar sudut di hadapan sisi b
b = panjang sisi b
C = besar sudut di hadapan sisi c
c = panjang sisi c
AP ┴ BC
BQ ┴ AC
CR ┴ AB
Perhatikan segitiga ACR
Sin A = CR/b maka CR = b sin A …(1)
Perhatikan segitiga BCR
Sin B = CR/a maka CR = a sin B …. (2)
Perhatikan segitiga ABP
Sin B = AP/c maka AP = c sin B … (3)
Perhatikan segitiga APC
Sin C = AP/b maka AP = b sin C …(4)
Berdasarkan persamaan (1) dan (2) didapat
CR = b sin A = a sin B maka a/sin A = b/sin B …(5)
Berdasarkan persamaan (3) dan (4) didapat
AP = c sin B = b sin C maka b/sin B = c/sin C …(6)
Kemudian, berdasarkan persamaan (5) dan (6) diperoleh
a/sin A = b/sin B = c/sin C
Persamaan ini yang kemudian disebut dengan aturan sinus.
Contoh Soal Aturan Sinus
1. Andi sedang mengukur mainan segitiganya yang tiap sudutnya dikodekan dengan A, B, dan C, kemudian diketahui segitiga tersebut memiliki sudut A = 30º, sisi a = 6cm dan sisi b = 8cm. Hitung besar sudut B!
Pembahasan
Akan dicari besar sudut B
sin B = (b sin A)/a
sin B = 8/6 sin 30̊
sin B = 2/3
B = arc sin B
B = arc sin (2/3)
B = 41,8̊
Jadi, besar sudut B adalah 41,8̊ atau 180̊ – 41,8̊ = 138,2̊
2. Sebuah segitiga ABC memiliki panjang AC = 4 cm. Jika besar ∠ ABC = 60º dan ∠BAC = 30º, maka panjang BC = … cm.
Pembahasan
AC/sin ∠ABC = BC/sin∠BAC
4cm/sin 60 = BC/sin30
4cm/½√3 = BC/½
BC = ½ × 4cm/½√3
BC = 4cm/√3
BC = 4/3 √3 cm
Jadi, panjang BC adalah BC4/3 √3cm.
3. Diketahui sebuah segitiga ABC dengan panjang AB = 9cm dan BC = 12cm. Jika besar ∠ ABC = 30º, tentukan luas segitiga ABC!
Pembahasan
L = ½ a t
- Misal a = AB, maka t adalah garis tegak lurus AB ke titik C berhadapan dengan ∠ ABC, maka
Sin ∠ABC = t/BC
t = BC × Sin ∠ABC
Sehingga diperoleh
L = ½ a t
L = ½ × AB × BC × Sin ∠ABC
L = ½ × 9cm × 12cm × Sin 30o
L = ½ × 9cm × 12cm × ½
L = 27cm2
- Misal a = BC, maka t adalah garis tegak lurus BC ke titik A berhadapan dengan ∠ ABC, maka
Sin ∠ABC = t/AB
t = AB × Sin ∠ABC
Sehingga diperoleh
L = ½ a t
L = ½ × BC × AB × Sin ∠ABC
L = ½ × 12cm × 9cm × Sin 30o
L = ½ × 12cm × 9cm × ½
L = 27cm
Jadi, luas segitiga ABC adalah 27cm2.
4. Diketahui sebuah segitiga PQR memiliki luas sebesar 96cm2. Jika panjang PR = 12cm dan besar ∠PRQ = 60º, tentukan panjang QR!
Pembahasan
L = ½ × PR × QR × Sin ∠PRQ
96cm2 = ½ × 12cm × QR × Sin 60o
96cm2 = ½ × 12cm × QR × ½√3
96cm2 = 4√3cm × QR
QR = 96cm2 ÷ 4√3cm
QR = 24/√3 cm
QR = 8√3cm
Jadi, panjang QR adalah 8√3cm.
5. Sebuah segitiga XYZ memiliki panjang XZ = 6cm dan YZ = 2√3cm. Jika besar ∠ XYZ = 60º, tentukan besar ∠YXZ !
Pembahasan
XZ/sin ∠XYZ = YZ/sin∠YXZ
6cm/sin 60 = 2√3cm/sin∠YXZ
6cm/½√3 = 2√3cm/sin∠YXZ
sin∠YXZ = 2√3cm × ½√3 ÷ 6cm
sin∠YXZ = 3/6
sin∠YXZ = ½
YXZ = arc sin (½)
YXZ = 30º
Jadi, besar ∠YXZ adalah 30º.
6. Diketahui sebuah segitiga ABC memiliki luas sebesar 6cm2. Jika panjang AB = 3cm dan BC = 4cm, tentukan besar ∠ABC!
pembahasan
L = ½ × AB × BC × Sin ∠ABC
6cm2 = ½ × 3cm × 4cm × Sin ∠ABC
6cm2 = 6cm2 × Sin ∠ABC
Sin ∠ABC = 1
ABC = arc sin (1)
ABC = 90º
Jadi, besar ∠ABC adalah 90º.
HALAMAN SELANJUTNYA:
Blog channel yang sekedar ingin berbagi, mohon maah jika terdapat kesamaan isi postingan, hal itu tidak terlepas dari hasil pencarian saat membutuhkan, dan saya share ulang.
ConversionConversion EmoticonEmoticon