Pembuktian Volume Limas ~ Aan Channel

Kalian sudah tahu bagaimana bentuk limas ? Yups tepat sekali, salah satu contoh yangterkenal adalah Piramid yang ada di Mesir. Tapi dalam postingan ini, saya tidak akan membahas Piramida, karena saya bukan ahli sejarah. Tulisan ini akan membahas bagaimana memperoleh rumus Volume Limas yaitu $\dfrac{1}{3} \times \text{ Luas Alas } \times \text{ tinggi}$ . Apabila diperhatikan, rumus volume tersebut mirip dengan rumus volume Prisma, di Prisma tidak ada $\dfrac{1}{3}$ . Dari mana datangnya $\dfrac{1}{3}$ ? Melalui tulisan ini, saya akan mencoba mencari dari mana rumus tersebut. Dalam pembuktian ini, saya melakukan pendekatan geometri. Perhatikan kubus ABCD.EFGH berikut ini.

Selanjutnya jika dibuat semua garis diagonal ruang pada kubus tersebut, maka akan terbentuk bangun ruang yang baru, yaitu Limas (lihat gambar di bawah ini).

Dari gambar di atas, terdapat 6 bangun Limas, yaitu Limas T.ABCD, Limas T.BCGF, Limas T.CDHG, Limas T.ADHE, Limas T.ABFE, dan Limas T.EFGH. Limas-limas tersebut memiliki bentuk alas yang sama, yaitu berbentuk persegi dengan panjang sisinya adalah $s$ serta meliki tinggi yang sama pula, yaitu $t = \dfrac{1}{2}s$ . Oleh karena itu, dapat disimpulkan bahwa

6 x Volume Limas = Volume Kubus

= $s^3$

= $s^2 \times s$

Volume Limas = 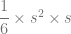$\dfrac{1}{6} \times s^2 \times s$

= $\dfrac{1}{6} \times s^2 \times 2t$

= $\dfrac{1}{3} \times s^2 \times t$

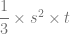
Karena alasnya berbentuk persegi dan luas persegi = 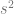$s^2$ , berakibat

= $\dfrac{1}{3} \times \text{ Luas Alas } \times \text{ tinggi}$

Jadi, terbukti bahwa Rumus Volume Limas adalah $\dfrac{1}{3} \times \text{ Luas Alas } \times \text{ tinggi}$

HALAMAN SELANJUTNYA:

About Aan Channel

Blog channel yang sekedar ingin berbagi, mohon maah jika terdapat kesamaan isi postingan, hal itu tidak terlepas dari hasil pencarian saat membutuhkan, dan saya share ulang.

Aan Channel

Pembuktian Volume Limas

About Aan Channel

Related Post